線形回帰をベイズ推定で解く（２）予測分布をプロット

線形回帰をベイズ推定で解く（１）予測分布の導出の続きです。今回は実際に予測分布をプロットして確認してみたいと思います。

まずは先回のおさらいですが、予測分布は

$p(t| x, \mathbf x, \mathbf t) = N(t |\boldsymbol \phi^{T}(x) \mathbf m_N, \sigma^{2} +\boldsymbol \phi^{T}(x) \mathbf S_N \boldsymbol \phi(x)) \tag{1}$

の式で与えられます。ここで $\mathbf m_N, \mathbf S_N$ は、

$\begin{eqnarray*} \displaystyle \mathbf{m}_N = \mathbf{S}_N \frac{1}{\sigma^2}\mathbf{X}^T \mathbf{t} \tag{2} \\ \displaystyle \mathbf S_N^{-1} = \frac{\mathbf X^T \mathbf X}{\sigma^{2}} + \frac{\mathbf I}{\sigma_0^{2}} \tag{3} \end{eqnarray*}$

です。 $\sigma^{2},\sigma_0^{2}$ はそれぞれ、訓練データと真値との誤差の分散、事前分布の分散を表します。

さっそく以上の式を使って様々な条件における予測分布を見てみましょう。

f:id:opabinia2:20180217220229p:plain （左）線形回帰を最小二乗法で解くなど、これまで線形回帰で扱ってきたものと同じ訓練データでベイズ推定してみました。今までは曲線が１つ決まっていましたが、予測確率の高いエリアがどこなのか？が見て取れます。

（中）意地悪で訓練データを数点取り除いてみました。訓練データがない部分は確信度が低くなっていることがわかります。これも今までの線形回帰なら確信度などは関係なく何らかの曲線が描かれていました。最尤推定なら最も尤度が高いところ、MAP推定なら事後確率が最も高いところ、という具合に。「最も高いところ」が他と比べて極めて高いのか、あるいはそれほど大差がないのか、そういう情報もベイズ線形回帰では表現できているんですね。

（右）もっと意地悪して訓練データを3点にしてみました。訓練データが少なすぎてほとんど予測不可能になっています。くどいですが、これも今までの線形回帰なら何らかの曲線が描かれていました。ベイズ推定では、精度が低いであろうことがはっきりとわかります。

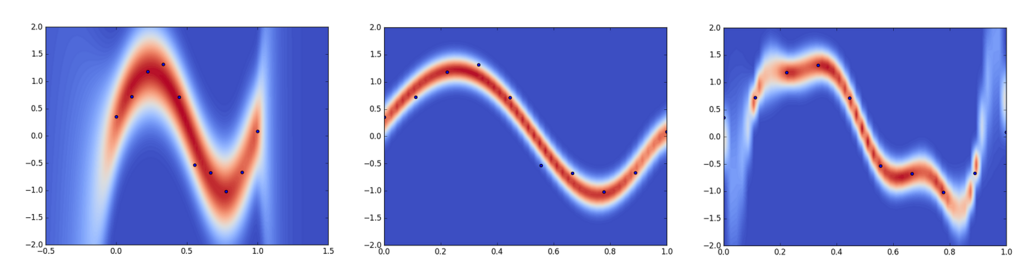f:id:opabinia2:20180217220241p:plain （左）横軸のプロット範囲を広げてみました。当たり前ですが、訓練データのない区間は予測不可能なことが確認できます。

（中）訓練データの分散 $\sigma^{2}$ を小さく見積もってみました。つまり、訓練データには誤差がほとんどのっておらず、信用度が高いと想定した場合です。これによって予測範囲狭まっていることが確認できます。

（右）さらに、事前分布の分散 $\sigma_0^{2}$ を大きな値にしてみました。事前分布の取りうる値の制約が弱いので過学習してしまっていることが確認できます。過学習しているときの曲線も線形回帰を最小二乗法で解くで確認したものと近いですが、その中でも確信度が低い部分があったりして面白いですね。

おまけ、、、この予測分布かっこよくないですか？ f:id:opabinia2:20180217220252p:plain f:id:opabinia2:20180217220529p:plain

今回使用したソースコード。誤差の分散は実際の値をカンニングして設定。事前分布の分散は適当に色々変えてグラフがそれっぽくなる値を選びました。こういう値の決め方も手法が存在するようです。

# ベイズ推定で予測分布を求める

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm


# 基底関数
def phi(x, M):
    return np.array([x**k for k in range(M+1)]).reshape(M+1, 1)


# 予測分布の値を返す
def normal(x, y):
    var = v + np.dot(phi(x, M).T, np.dot(SN, phi(x, M)))
    mu = np.dot(phi(x, M).T, mN)
    return (1/np.sqrt(2*np.pi*var))*np.exp(-((y-mu)**2)/(2*var))


vec_normal = np.vectorize(normal)

# ランダムシードを固定
np.random.seed(0)
# 多項式の最大べき乗数(x^0+...+x^M)
M = 9
# 訓練データ数
N = 10

# 訓練データの列ベクトル
x = np.linspace(0, 1, N).reshape(N, 1)

# 訓練データtの列ベクトル
t = np.sin(2*np.pi*x.T) + np.random.normal(0, 0.2, N)
t = t.reshape(N, 1)

# 行列Phiを作成
Phi = np.empty((N, M+1))
for i in range(M+1):
    Phi[:, i] = x.reshape(1, N) ** i

# 事前分布の分散
v0 = 1000
# 想定する誤差の分散
v = 0.2

# SN
SN = np.linalg.inv(1/v0 * np.eye(M+1) + 1/v*np.dot(Phi.T, Phi))

# mN
mN = 1/v*np.dot(SN, np.dot(Phi.T, t))

# 予測分布を求める
x_p, y_p = np.meshgrid(np.linspace(-0.5, 1.5, 100), np.linspace(-2.0, 2.0, 100))
z = vec_normal(x_p, y_p)

# 結果の表示
plt.xlim(0, 1)
plt.ylim(-2.0, 2.0)
plt.contourf(x_p, y_p, z,100, cmap=cm.coolwarm) #cm.gist_heatにするとかっこいい
plt.scatter(x, t)
plt.show()

機械学習に詳しくなりたいブログ

機械学習や数学について勉強した内容を中心に書きます。100％趣味です。記事は数学的に厳密でなかったり誤りを含んでいるかもしれません。ご指摘頂ければ幸いです。

線形回帰をベイズ推定で解く（２）予測分布をプロット