今回は多変量正規分布をMCMC法でサンプリングしてみました。MCMC法の理論背景などはこちらの記事です。こちらで書いたコードを少し修正するだけなので実装は簡単です。多変量正規分布で書いた分散共分散行列が
のものをサンプリングしてみます。平均は0としました。また、提案分布も先回同様に正規分布を用いたものにしました。
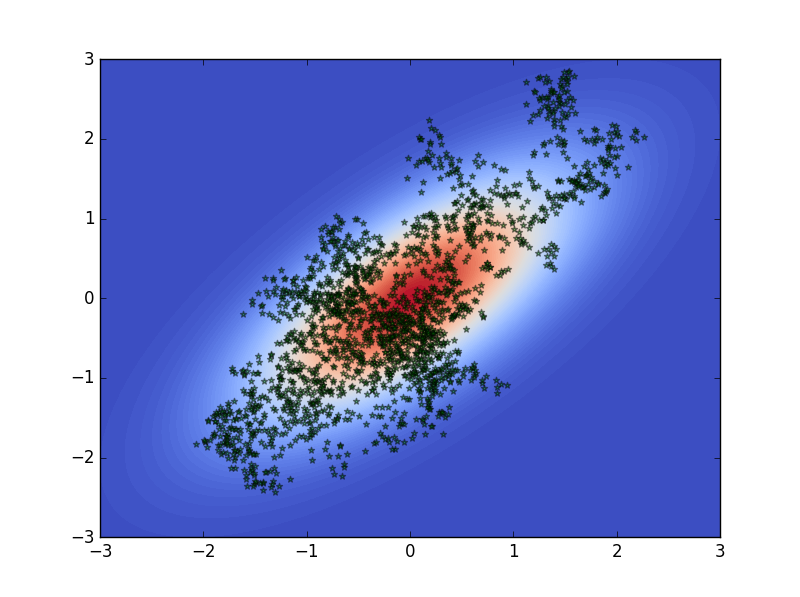
 うまくサンプリングできていますね。先回同様、提案分布の分散が適切でないと、以下のようにサンプリングがうまくいかない場合があります。分散が小さすぎて分布全体からサンプリングできていません。
うまくサンプリングできていますね。先回同様、提案分布の分散が適切でないと、以下のようにサンプリングがうまくいかない場合があります。分散が小さすぎて分布全体からサンプリングできていません。
今回のコードです。多変量正規分布だと面白くないのでもうちょっと違う分布も試してみたいですね。面白い形の関数ないかな。
# マルコフ連鎖モンテカルロ法(メトロポリスヘイスティングス法)のテスト import numpy as np import matplotlib.pyplot as plt from matplotlib import cm # 目標分布(多変量正規分布)の分散共分散行列 s = np.array([[1, 0.7], [0.7, 1]]) # 提案分布 def q(x): mu= [0, 0] cov = [[0.5, 0], [0, 0.5]] z = np.random.multivariate_normal(mu, cov).T return x + z # サンプルしたい関数 def p(x1, x2): x = np.array([x1, x2]) return (1/np.sqrt((2*np.pi)**2*np.linalg.det(s))) * np.exp(-0.5*np.dot(np.dot(x.T,np.linalg.inv(s)),x)) # MCMC def MCMC(x): # サンプル候補 z = q(x) if p(z[0], z[1])/p(x[0], x[1]) > np.random.uniform(0, 1): return z else: return x vec_p = np.vectorize(p) # ランダムシードを固定 np.random.seed(0) # サンプル数 N = 3000 # バーンイン B = 1000 # 初期値 x = np.array([2, 2]) samples = np.empty([N, 2]) # MCMC for i in range(N): x = MCMC(x) samples[i, :] = x x, y = np.meshgrid(np.linspace(-3, 3, 100), np.linspace(-3, 3, 100)) z = vec_p(x, y) plt.contourf(x, y, z, 100, cmap=cm.coolwarm) plt.scatter(samples[B:, 0], samples[B:, 1],c="green", marker="*",alpha=0.5) plt.xlim(-3, 3) plt.ylim(-3, 3) plt.show()