ニュートン法（1変数の場合）

概要

ニュートン法は、 $f(x)=0$ の解 $\alpha$ を求める数値計算法で、最急降下法に比べて収束が早い特徴があります。ニュートン・ラフソン法とも呼びます。

アルゴリズム

関数 $f(x)$ の点 $x_n$ における接線 $g(x)$ は以下の式で与えられます。

$g(x) = f^{\prime}(x_n)(x-x_n)+f(x_n) \tag{1}$

式(1)の接線と、 $x$ 軸との交点は

$\begin{eqnarray*} f^{\prime}(x_n)(x-x_n)+f(x_n) &=&0\tag{2} \\ \displaystyle x &=& x_n - \frac{f(x_n)}{f^{\prime}(x_n)} \tag{3} \end{eqnarray*}$

です。接線は関数 $f(x)$ の1次近似ですから、式(3)で表される交点は $f(x)$ を1次近似した場合における $f(x)=0$ の解であると考えられます。その近似解は $x_n$ よりも真の解に近づいていると想定されます。したがって、得られた近似解において、さらに式(3)によってより確からしい近似解を得ることができます。このようにして繰り返し更新することで真の解に近づいていくことができます。図で表すと以下のようなイメージです。

青色の線が関数 $f(x)$ 、オレンジが接線 $g(x)$ です。適当な初期値 $x_n$ における接線と $x$ 軸との交点 $x_{n+1}$ が式(3)によって得られ、これを繰り返すことで解 $\alpha$ に近づいていきます。

ここで、 $f^{\prime}(x)=0$ となる点が求めたい場合は、

$\displaystyle x = x_n - \frac{f^{\prime}(x_n)}{f^{\prime \prime}(x_n)} \tag{4}$

とすれば良いです。

$f(x)=0$ の解 $\alpha$ を求めるニュートン法のアルゴリズム

$x$ の初期値を設定する。
$\displaystyle x_{new} = x_{old} - \frac{f(x_{old})}{f^{\prime}(x_{old})}$ 　によって $x$ を更新する
停止条件（更新量が一定値以下になるなど）が満たされるまで手順２を繰り返す

実験

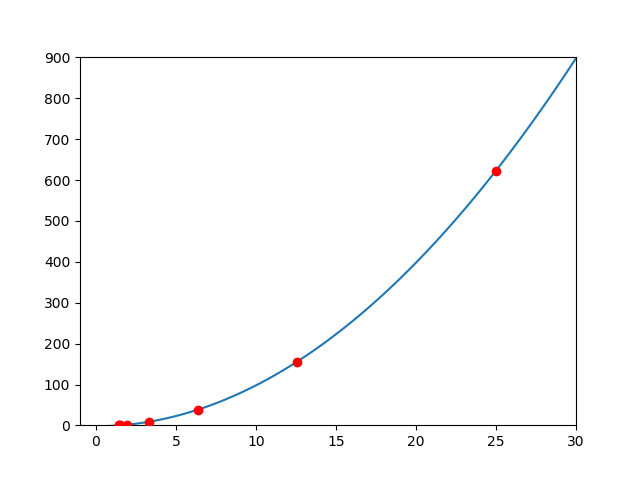
試しに $x^{2} -2=0$ の解 $\sqrt{2}$ をニュートン法で求めてみまた。数回の反復で1.4142135623...が得られました。仮に初期値を25としてみたとき、解への近づき方は以下のグラフのようになり、収束の早さが見て取れます。

テストしたコード。今回は反復回数を固定にしていますが、実際は適当な停止条件を設けて計算するようです。また、初期値が解から遠いと、収束しない場合もあるとのこと。 $x^{2} -2=0$ は単純なのでどんな初期値からでも解が求められそうですが。

# ニュートン法
import numpy as np

def f(x):
    return x**2 - 2

def newton(xn):
    return f(xn)/(2*xn)


# 初期値
x = 3.0

# ニュートン法による更新
for i in range(10):
    x -= newton(x)
    print(x)