ガウス過程による分類（７）実験結果 - 機械学習に詳しくなりたいブログ

ガウス過程による分類（１）～（６）までの長い道のりを経て、ようやく以下の式が得られました。

$\displaystyle p(t_{N+1}=1 | \mathbf{t}_{N} )\simeq \sigma \left( \frac{\mathbf{k}^{T}\mathbf{C}_{N}(\mathbf{t}_{N}-\boldsymbol {\sigma}_{N})}{1+\displaystyle \frac{\pi}{8}\left\{ c-\mathbf{k}^{T}(\mathbf{W}_{N}^{-1}+\mathbf{C}_{N})\mathbf{k} \right\} } \right) \tag{1}$

今回はこれを使って予測分布を求めてみたいと思います。おさらいですが、各文字は以下のようなものでした。

$\mathbf{C}_{N}$ は各要素が式(2)の行列。

$C(x_{n},x_{m}) = k(x_{n},x_{m}) + \nu \delta_{nm} \tag{2}$

$\mathbf{k} = ( k(\mathbf{x_{1}},\mathbf{x_{N}}) , \cdots , k(\mathbf{x_{N}},\mathbf{x_{N}}))^{T} \tag{3}$

$c = k(\mathbf{x_{N+1}},\mathbf{x_{N+1}}) + \nu \tag{4}$

$\boldsymbol {\sigma}_{N} = (\sigma(a_{1}), \cdots, \sigma(a_{N})) \tag{5}$

$\mathbf{w}_{N} = \left( \begin{array}{cccc} \sigma(a_{1})(1-\sigma(a_{1})) & & & 0 \\ & & \ddots & \\ 0 & & & \sigma(a_{N})(1-\sigma(a_{N})) \end{array} \right) \tag{6}$

式(5)、(6)は、ニュートン法により求める $\nabla \Psi(\mathbf{a}_{N}^{\prime})=\mathbf{0}$ となる点 $\mathbf{a}_{N}^{\prime}$ を使います。

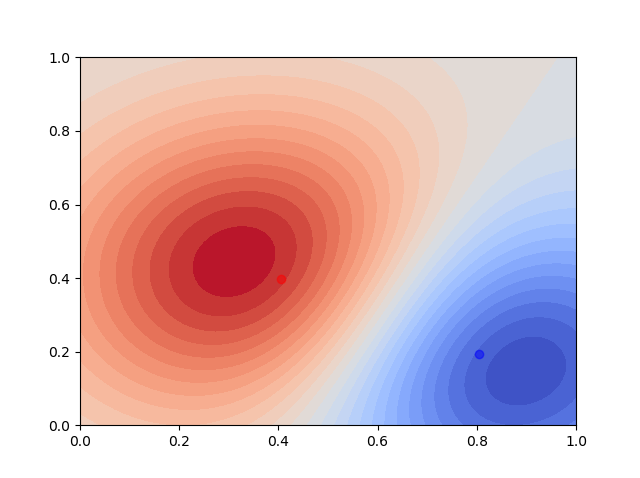
では結果です。 f:id:opabinia2:20200104134317p:plain ガウスカーネルの $\sigma$ を小さくしてみると次のようになりました。 f:id:opabinia2:20200104134324p:plain 結果の図だけ見るとカーネル回帰分析（２）実験結果と似たような感じですね。

訓練データを２点にした結果を見ると、何が行われているのかよくわかります。点を中心としてガウスカーネルが配置されているようなイメージです。中心が少しずれているのは互いの点の影響を受けているためと思います。 f:id:opabinia2:20200104134334p:plain

入力を非線形変換したロジスティック回帰でもガウス基底を使って識別をしていましたが、これは基底を自分で適切に設定しなければなりませんでした。一方カーネル法では無限次元の特徴を持つガウスカーネルを使えば、基底をどう設定するか、ということに頭を使わなくてよくなってしまうんですね。

今回のコードです。ニュートン法のイテレーションは適当に10回固定としています。

# ガウス過程による分類
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm


# 教師データ
def create_data(x,y):
    if y > -2*x +1 and y > 2*x -1 :
        return 1
    else:
        return 0


# カーネル関数
def kernel(x0, x1):
    sigma = 0.3
    return np.exp(- np.linalg.norm(x0-x1) ** 2 / (2 * sigma ** 2))


# グラム行列
def gram_matrix(x):
    gram = np.empty([N, N])
    for i in range(N):
        for j in range(N):
            gram[i, j] = kernel(x[:,i], x[:,j])
    return gram


def sigmoid(a):
    return 1/(1+np.exp(-a))


# 予測分布
def p_tt(x2, y2):
    # kを求める
    k = np.zeros(N)
    for i in range(N):
        k[i] = kernel(x[:, i], np.array([x2, y2]))

    mu = k @ (t-sigma_N)
    v = kernel(np.array([x2, y2]), np.array([x2, y2])) - k @ np.linalg.inv(np.linalg.inv(WN)+CN) @ k
    return sigmoid(mu/np.sqrt(1+(np.pi*v)/8))


# ランダムシードを固定
np.random.seed(0)

# 行列Cに加えるノイズ
NU = 0.1

# 訓練データ点数
N = 100

# 2クラス分のデータを作成
x = np.random.uniform(0, 1, [2, N])
t = np.empty([N])
t = np.vectorize(create_data)(x[0, :], x[1, :])

# a' をニュートン法で求める

# a の初期化
a = np.random.uniform(-1,1,N)

# CNを求める
CN = gram_matrix(x) + NU * np.eye(N)

# ニュートン法の繰り返し
for i in range(10):
    # sigma_N
    sigma_N = sigmoid(a)
    # WNを求める
    WN = np.diag(sigmoid(a)*(1 - sigmoid(a)))
    # aの更新
    a = CN @ np.linalg.inv((np.eye(N) + WN @ CN)) @ (t - sigma_N + WN @ a)


#新たな入力
x2, y2 = np.meshgrid(np.linspace(0, 1, 100), np.linspace(0, 1, 100))

# 予測値を計算
result = np.vectorize(p_tt)(x2, y2)


plt.xlim(0, 1)
plt.ylim(0, 1)
plt.contourf(x2, y2, result,30, cmap=cm.coolwarm)
plt.scatter(x[:,np.where(t==1)][0], x[:,np.where(t==1)][1], color="red", alpha=0.5)
plt.scatter(x[:,np.where(t==0)][0], x[:,np.where(t==0)][1], color="blue", alpha=0.5)
plt.show()